Article Text
Abstract
In two 1959 papers, one coauthored, Jerome Cornfield asserts that ‘relative’ measures are more useful for causal inference while ‘absolute’ measures are more useful for public health purposes. In one of these papers (the single-authored one), he asks how epidemiology should respond to the fact that its domain is not a highly ‘articulated’ one—it is not susceptible to being subsumed under general laws. What is the connection between these issues? There has recently been some backlash against ‘risk relativism’, and Charles Poole has recently dismantled the mathematical argument for the first claim. However the problem with ‘Cornfield's Principle’ seems to go much deeper. The whole attempt to partition measures into absolute and relative is fundamentally mistaken. Why, then, has it seemed so appealing? Perhaps one reason is the influence that early education in the physical sciences continues to exert on the way epidemiologists think, and their response to the low articulation of their domain of study.
- EPIDEMIOLOGY
- PUBLIC HEALTH
- Epidemiological methods
Statistics from Altmetric.com
Recently, a number of authors have commented on ‘risk relativism’, a tendency of epidemiologists to express strength of association using relative risk, or to emphasise the importance of that measure over others for causal inference purposes.1 ‘Relative’ measures seem to be more commonly reported in mainstream media as well. What is ‘risk relativism’, and what explains it? In this short piece I seek to summarise some of the explanations that have been proposed, and to suggest a slightly different (though not necessarily incompatible) explanation. In a nutshell, I will argue that risk relativism arises from a sort of ‘physics envy’, giving rise to a desire to formulate universal law-like claims.
Charles Poole has recently offered an interesting explanation for risk relativism.1 He traces this tendency to a decisive intervention in the debate about the causality of the association between smoking and lung cancer.
A serious difficulty for establishing the causality of the association between smoking and lung cancer was the fact that smoking appeared to be associated with many other diseases as well. As Joseph Berkson put it in 1958:
…some other explanation must be formulated for the multiple statistical associations found with so wide a variety of categories of disease. And if we are not to crassly violate Occam's razor, we should not attribute to each separate association a radically different explanation.2
The reasoning is appealing. At the time, there was evidence that tar painted onto the ears of rats caused tumours. So perhaps exposure to smoke containing tar might cause cancer of the lung. But then what of bladder cancer or coronary heart disease? Clearly, neither arises from direct exposure to smoke. Would it not be a grand coincidence if smoking also initiated several other unrelated processes leading to deleterious health outcomes?
There are two salient options for resisting Berkson's point. One is to insist that smoking does indeed violate Occam's razor in this way—that it is bad for us in a number of different ways. The other is to insist that there can be evidence that one of the associations is causal, even if the others are unexplained.
We now know that the former is correct. However, the latter is the option that epidemiological and statistical luminaries of the day selected. Jerome Cornfield and his co-authors made a mathematical argument that relative risk is of particular use in eliminating potential confounders.3 This afforded a basis for inferring causality in the lung cancer/smoking associations even while the other associations were not thereby explained, because the lung cancer association exhibited a particularly high relative risk. They summarise their position in what we might, for convenience rather than with the intention of crediting it solely to him, dub Cornfield's Principle:
The relative measure is helpful in … appraising the importance of an agent with respect to other possible agents inducing the same effect … The absolute measure would be important in appraising the public health significance of an effect known to be causal.3
Cornfield's Principle is influential, and replicated in a number of places.4 Yet it turns out that the principle is incorrect, even though the conclusion that the authors used it to reach—that smoking causes lung cancer—is evidently right.
What is wrong with Cornfield's Principle? Poole has already pointed out one problem: the mathematical arguments that Cornfield et al advanced concerning the use of relative risk to eliminate potential confounders can be replicated for risk difference. Poole conjectures that had this been noticed earlier, the association between smoking and heart disease—much more important for public health—might have been accepted as causal much sooner.
However the problem with Cornfield et al's Principle goes deeper than this mathematical slip-up. An association that is pronounced large in ‘relative’ terms may turn out to be small if another ‘relative’ measure is used, and vice versa. Again, let us revert to Berkson:
If … heart disease, independently of smoking, causes a greater number of deaths than lung cancer does, then smoking would have fewer susceptibles to kill with heart disease than with cancer of the lung. In that case, a given number of deaths from heart disease, attributed to smoking, would reflect a greater mortal force for heart disease than the same number of deaths would reflect for cancer of the lung.2
Suppose we measure the ‘mortal force’ of the exposure by the ratio of the complements of risk among unexposed (RU) to risk among exposed (RE). This measure is known as the survival proportion,5 but to link with Berkson's wording, we could also call it a susceptibility ratio (SR):
SR tells us how many times larger the healthy unexposed population is than the healthy exposed population. The larger the SR is, the stronger the (damaging) effect of the exposure.
Suppose RU for lung cancer is 0.005 and RE is 0.1, then relative risk is 20 (=0.1/0.005), but SR is only 1.11 (=(1–0.005)/(1–0.1)). Compare coronary heart disease. Suppose RU is 0.13 and RE is 0.22. The relative risk is 1.69 (=0.22/0.13), but SR is 1.12 (=(1–0.13)/(1–0.22)).
These figures are fictitious—they are for illustration only. However they illustrate the possibility that the rank order of measured ‘strengths’ might reverse with choice of a different measure. Yet SR is as much a ‘relative’ measure as relative risk: it is a ratio and a function of RE and RU alone (we can replace 1 with RE/RE or RU/RU). It is not the case, on these figures, that the ‘relative’ effect of smoking on lung cancer is much larger than smoking on heart disease. It all depends which ‘relative’ measure is used.
The underlying reason is that the distinction between ‘absolute’ and ‘relative’ measures is unreal. The distinction might be thought to depend on any one of a number of equally plausible factors. Let us consider two candidates: whether the measure is a difference or a ratio; and whether it is a function of prevalence of exposure. In this connection, compare population-attributable risk and risk difference. Which is more ‘absolute’ and which more ‘relative’? The former but not the latter is a function of prevalence of exposure, so absolute in that regard. Yet the former but not the latter is a ratio, so relative in that regard. It is simply unclear that any helpful, non-arbitrary distinction between absolute and relative measures can be drawn. Not only is Cornfield’s Principle mistaken to claim that relative measures are especially useful for causal inference (as Poole points out), it is mistaken to partition measures into relative and absolute in the first place. Of course, we could arrive at a neat distinction between ‘relative’ and ‘absolute’ measures by definition—that is, by simply postulating such a distinction. As Bertrand Russell6 puts it, “the method of ‘postulating’ what we want has many advantages; they are the same as the advantages of theft over honest toil.” The possibility of drawing a sharp distinction does not show that there exists an objective basis for the distinction. And indeed in this case it seems there just is no objective basis for dividing the measures in one of the ways just countenanced rather than another.
If Cornfield’s Principle is mistaken, what explains its appeal to Cornfield and his colleagues, its persuasiveness at the time and its persistence since? No doubt the statistical convenience of estimating relative risks from ORs plays a role.7 However that cannot explain the whole of risk relativism, because it does not explain the claim that relative measures are more appropriate for certain uses, and absolute for others.
A meatier idea is that relative risks are transportable between populations, more so than other measures. If the level of risk in a given population is low, then the risk difference will be low, since RE and RU will necessarily be low, and the difference between two small numbers is another small number. (To illustrate another way, risk difference cannot exceed total risk, which would have to happen if a large enough risk difference were ‘transported’ to a population with low total risk.) However the ratio between two small numbers can be as large as the ratio between two large numbers: so the same relative risk might hold regardless of total population risk and independent of the prevalence of exposure.
However, the transportability of risk ratios between populations cannot be assumed from the mere fact that transportability is a mathematical possibility, since that transportability relies on the absence of multiplicative interaction, which implies the presence of additive interaction5—something of considerable public health interest, incidentally.8 Practically speaking, we want to measure, not ignore additive interaction. And from our present, theoretical perspective, the relation between additive and multiplicative interaction shows that transportability of risk ratios is an empirical rather than a conceptual thesis: it is not explained by the nature of relative risk (as the reasoning of the previous paragraph might lead us to hope), but rather arises from properties of the populations in question.
A more speculative explanation for risk relativism is that epidemiology labours under the long shadow of theoretical physics. Expressing an association using relative risk is the closest we might come to expressing something like a law: it may appear, misleadingly, to extract a measure of the ‘force’ of an exposure from population-specific information, and thus to be more suited to ‘purely scientific’ purposes such as causal inference. On the other hand, measures which wear their population-specificity on their sleeve, such as population-attributable fraction, are more likely to be seen as impure, applied and practical.
Support for this hypothesis might be discerned in Cornfield's ‘other’ 1959 paper. This paper is better known for its discussion of randomised controlled trials, but it also contains lengthy passages in which Cornfield seeks to understand the challenges facing a science such as epidemiology that studies a domain of low ‘articulation’, that is, a domain that is not readily subsumed under general laws.9 It is striking that Cornfield starts by asking what a scientist must aim for in a domain of low articulation, and then, a few pages later, identifies a special role for relative risk—a role in guiding us to facts that are more general and less population specific.
We have seen already that the mathematical reasons for which relative risk was supposed to guide us to causal relations are not in fact specific to relative risk. However we might take our speculation one step further than anything Cornfield actually says, and ask whether relative risk might, in principle, enable not merely the discovery of causal relations but the expression of epidemiological laws as well. That speculation would satisfy the idea that relative risk is of special scientific significance, even where its public health significance is limited, as well as the idea countenanced earlier, that relative risks might be more transportable.
What would an epidemiological law look like? Such a law might feature relative risk as a constant: we might say, for instance, that it is a law that the relative risk of lung cancer among male smokers compared with male non-smokers is 20. We could even express this as a simple equation: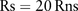
With suitable circumscribing conditions (eg, Rs, lifetime risk among male smokers; and Rns, lifetime risk among male non-smokers) the constant would be a property of the exposure, in contrast to facts about the populations in question—prevalence of exposure, absolute risk levels, etc. Variations from the calculated value in particular populations might be attributed to the interference of other factors, much as the failure of Newtonian equations of motion in everyday life is attributed to friction. Relative risk might exert a fascination precisely because it comes closer than any other measure to enabling the formulation of epidemiological laws along these lines. (Of course, the mere possibility of formulating a relationship in this way does not prove that the relationship is a law. However, we do expect laws to be such that they can be formulated this way, at least if they fit the mould of universal laws exemplified by physical laws. Expressibility in this form is not sufficient for lawhood, as philosophers will say; but it is a plausible necessary condition.)
The formulation of such laws implies that the measures invoked express properties of the exposure, not of the population. Formulating general properties of causal factors in population-independent laws is a possibility that has been strenuously denied by some statisticians10 and philosophers,11 regarding the social sciences in general, on general grounds of the complexity of the social world. This complexity is supposed to mean that we simply would not find any sort of situation like the one described in the foregoing paragraph. However it is not clear that such an argument refutes the extreme sort of risk relativism countenanced here. For one thing, Cornfield is evidently aware of the relatively unarticulated nature of the epidemiological domain, as he would put it. However more importantly, the complexity-driven argument is highly contingent. What becomes of the complexity argument if, as it happens, we find that relative risk (RR) for lung cancer among smokers and non-smokers is indeed relatively constant between populations? It will have been refuted for this domain.
Perhaps a more fruitful way to think about the extreme form of risk relativism hypothesised here is to ask where the aspiration to identify laws of epidemiology might come from. It is characteristic of epidemiology to blur the distinction between pure science and practical endeavour.12 The greatest epidemiological discoveries have also been its greatest contributions to public health. Yet the sciences taught in schools—physics, chemistry and biology—are mostly quite different from epidemiology. They seek general, universal laws, not expressions of population-specific facts. These are the sciences that shape our ideas about what distinguishes science from stamp collecting. And in these sciences, Occam's razor wields considerable influence. By the time epidemiological education begins, childhood is over, and with it the most significant opportunities to exert deep influence on the way we think. Perhaps Cornfield's Principle is a symptom of this early educational experience. If so, it is an intellectual aspiration, a way of thinking—a matter of values, albeit intellectual values, rather than facts. And if so, then it cannot be refuted. Perhaps it will continue to exert an influence unless or until sciences such as epidemiology are more widely taught in schools.
Acknowledgments
The author is grateful to Jonathan Fuller, Dan Heard, Alfredo Morabia, Dean Peters and Jan Vandebroucke for helpful discussions and to the audience at the workshop ‘Prediction in Epidemiology and Healthcare’ held at King's College London in June 2014 for their comments.
Footnotes
-
Funding National Research Foundation of South Africa.
-
Competing interests None.
-
Provenance and peer review Commissioned; externally peer reviewed.


